cours de physique terminale D
Chapitre : 1./ Électricité et Magnétisme
En Terminale D, le chapitre d'Électricité et Magnétisme est crucial, couvrant plusieurs concepts fondamentaux sur les interactions entre charges électriques et champs magnétiques. Voici les principaux sous-thèmes :
1. Loi de Coulomb et Champ Électrique
. Loi de Coulomb : Elle décrit la force 𝐹 entre deux charges ponctuelles 𝑞1 et 𝑞2 situées à une distance 𝑟 l'une de l'autre dans le vide. La formule est donnée par :
𝐹=𝑘𝑒(𝑞1⋅𝑞2)/𝑟2 où 𝑘𝑒 est la constante de Coulomb (≈8,99×10^9 N m2 / C2).
Champ Électrique 𝐸 : Le champ électrique créé par une charge ponctuelle 𝑞 à une distance 𝑟 est donné par :
𝐸=𝑘𝑒(𝑞/𝑟^2)
Ce champ est un vecteur qui représente l'influence qu'exerce une charge sur l’espace environnant.

2. Potentiel Électrique
. Définition du Potentiel Électrique : Le potentiel électrique en un point est l’énergie potentielle électrique par unité de charge. Il est calculé pour une charge 𝑞 par rapport à un point de référence (généralement l'infini).
. Relation avec le Champ Électrique : Le champ électrique est lié au gradient du potentiel électrique, et une variation de potentiel entre deux points crée une force qui déplace les charges.

3. Loi d'Ohm et Circuits Électriques
* Loi d'Ohm : Elle relie la tension 𝑉, l’intensité 𝐼, et la résistance 𝑅 d’un conducteur par la formule : 𝑉=𝐼⋅𝑅
* Résistances en Série et en Parallèle :
- Série : 𝑅equiv=𝑅1+𝑅2+⋯+𝑅𝑛
- Parallèle : 1/𝑅équiv=1/𝑅1+1/𝑅2+⋯+1/𝑅𝑛
* Loi de Kirchhoff :
- Première loi (des nœuds) : La somme des courants qui entrent dans un nœud est égale à la somme des courants qui en sortent.
- Deuxième loi (des mailles) : Dans une boucle fermée, la somme des tensions est nulle.

4. Champ Magnétique et Force de Lorentz
Champ Magnétique 𝐵 : Une charge en mouvement ou un courant crée un champ magnétique dans l’espace environnant. Ce champ est un vecteur mesuré en teslas (T).
Force de Lorentz : Lorsqu'une charge 𝑞 se déplace à une vitesse 𝑣 dans un champ magnétique 𝐵, elle subit une force 𝐹 perpendiculaire à 𝑣 et 𝐵, définie par :𝐹=𝑞𝑣⃗×𝐵⃗
Cette force est la base des moteurs électriques et autres applications.

5. Induction Électromagnétique
* Loi de Faraday : Elle décrit comment un champ magnétique variable dans le temps induit une tension dans un circuit. La formule est :
𝐸=−𝑑Φ/𝑑𝑡 où Φ est le flux magnétique et 𝐸 est la force électromotrice induite.
* Loi de Lenz : Elle indique que le sens du courant induit dans un circuit est tel qu’il s’oppose à la variation du flux magnétique qui l’a produit.

6. Applications Pratiques : Transformateurs et Moteurs
* Transformateurs : Utilisés pour augmenter ou diminuer la tension dans les réseaux électriques. Ils fonctionnent grâce à l’induction entre les bobines primaire et secondaire.
* Moteurs et Générateurs : Les moteurs électriques utilisent l'interaction entre un courant et un champ magnétique pour produire un mouvement, tandis que les générateurs convertissent le mouvement en électricité via l'induction.
* Approche Expérimentale
Ce chapitre inclut de nombreuses expérimentations pratiques comme la mesure de la force entre charges, l’observation des champs magnétiques autour d’aimants ou de conducteurs, et des exercices sur les circuits électriques. Ces activités visent à renforcer la compréhension des phénomènes et des lois.
Ces concepts de l'électricité et du magnétisme permettent aux étudiants de comprendre les bases des systèmes électriques et magnétiques modernes, servant de fondement pour des études plus avancées en physique ou en ingénierie.
Exercice 1 : Calcul de la Force Électrique
Deux charges ponctuelles 𝑞1=3𝜇𝐶 et 𝑞2=−2𝜇𝐶 sont placées à une distance de
10cm l'une de l'autre dans le vide.
Calculez la force électrique 𝐹 entre 𝑞1 et 𝑞2 en utilisant la loi de Coulomb.
Indiquez si cette force est attractive ou répulsive.
Indications : Utilisez 𝑘𝑒=8,99×10^9 N m2 / C2 .
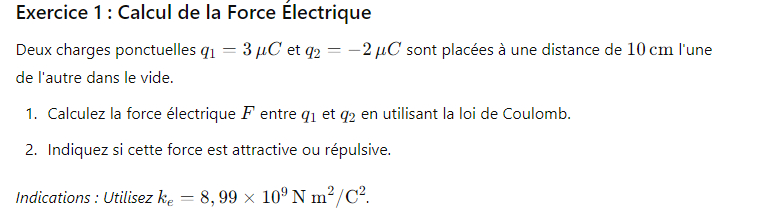
Exercice 2 : Étude d’un Circuit Électrique en Série
On dispose de trois résistances
𝑅1=10Ω,
𝑅2=20Ω, et
𝑅3=30Ω, connectées en série dans un circuit alimenté par une source de tension de 𝑉=12𝑉.
Calculez la résistance équivalente du circuit.
Trouvez l’intensité du courant dans le circuit.
Déterminez la tension aux bornes de chaque résistance.

Exercice 3 : Loi de Kirchhoff
Dans un circuit avec deux branches, les courants 𝐼1 et 𝐼2 se rejoignent en un nœud pour former le courant 𝐼3 dans une troisième branche. Supposons que
𝐼1=3A et 𝐼2=2A.
1. En utilisant la première loi de Kirchhoff (somme des courants), trouvez
𝐼3.
2. Si la résistance totale de la troisième branche est
𝑅=4Ω, calculez la tension 𝑉 dans cette branche.

Exercice 4 : Induction Électromagnétique
Un conducteur droit de longueur 𝐿=0,5m se déplace dans un champ magnétique uniforme de 𝐵=0,2T avec une vitesse 𝑣=3m/s, perpendiculairement au champ magnétique.
1. Calculez la force électromotrice (fem) induite dans le conducteur.
2. Indiquez le sens du courant induit si la direction du champ magnétique est vers l'intérieur de la feuille.

Exercice 5 : Calcul de l'Énergie Stockée dans un Condensateur
Un condensateur de capacité 𝐶=10𝜇𝐹 est chargé à une tension de 𝑉=100𝑉.
1. Calculez l'énergie 𝐸 stockée dans le condensateur.
2. Si la charge est doublée, de combien l’énergie stockée augmentera-t-elle ?
Formule : 𝐸=1/2𝐶𝑉^2

Exercice 6 : Moteur à Courant Continu et Force de Lorentz
Une boucle de fil rectangulaire de longueur 𝑙=0,2m et largeur 𝑤=0,1m porte un courant 𝐼=2A dans un champ magnétique 𝐵=0,3T. La boucle est orientée de sorte que le champ magnétique est perpendiculaire à la surface de la boucle.
1. Calculez la force exercée sur chaque segment de la boucle.
2. Déterminez le moment de force agissant sur la boucle.

Correction Exercice 1 : Calcul de la Force Électrique

Correction exercice 2 : Étude d’un Circuit Électrique en Série

Correction Exercice 3 : Loi de Kirchhoff

Correction Exercice 4 : Induction Électromagnétique

Correction Exercice 5 : Calcul de l'Énergie Stockée dans un Condensateur

Correction Exercice 6 : Moteur à Courant Continu et Force de Lorentz

Livre PDF, annales Sciences Physiques Terminale D
Autres cours et formations pouvant vous interressés

Cours de mathématiques terminale D
Cours de mathématiques terminale D
Le programme de mathématiques de la Terminale D au Burkina Faso suit les exigences du système éducatif national et aborde divers chapitres dans le but de préparer les étudiants au Baccalauréat. Voici un aperçu des principaux thèmes qui sont généralement couverts :
1. Algèbre et Analyse
Étude des fonctions :
Fonctions polynomiales, rationnelles, exponentielles, logarithmiques.
Fonctions dérivables et continuité.
Limites et asymptotes.
Dérivées et études des variations des fonctions.
Équations et inéquations :
Résolution d'équations polynomiales et rationnelles.
Inéquations du premier et du second degré.
Suites numériques :
Suites arithmétiques et géométriques.
Limites de suites.
Intégration :
Calcul d’intégrales simples et applications (aire sous une courbe).
2. Géométrie
Vecteurs et produits scalaires :
Notions de base sur les vecteurs dans le plan et l’espace.
Produit scalaire, norme, orthogonalité.
Géométrie dans l’espace :
Plans et droites dans l’espace.
Distance, projections orthogonales, angle entre deux droites, entre un plan et une droite.
Géométrie analytique :
Coordonnées dans le plan et l’espace.
Équations des droites, plans, et cercles.
3. Probabilités et Statistiques
Probabilités :
Expériences aléatoires, espaces probabilisés.
Loi des probabilités, probabilité conditionnelle, indépendance.
Loi binomiale et loi normale.
Statistiques :
Notions de base : moyenne, variance, écart-type.
Distribution de fréquences et représentations graphiques.
Échantillonnage et estimation.
4. Arithmétique
Nombres entiers et divisibilité.
Congruences, théorème de Bézout.
Nombres premiers, décomposition en facteurs premiers.
5. Complexes
Nombres complexes : forme algébrique et trigonométrique.
Opérations sur les complexes (addition, multiplication, division).
Module et argument, exponentielle complexe.
Résolution d’équations dans les complexes.
6. Algorithmique
Initiation à l’algorithmique : variables, boucles, conditionnelles.
Résolution de problèmes simples avec des algorithmes.
7. Exercices pratiques et préparation au Baccalauréat
Travaux dirigés et exercices types Bac.
Résolution d’exercices de synthèse pour se préparer aux épreuves.
Épreuve du Bac
L'épreuve de mathématiques est généralement écrite et dure environ 4 heures. Elle consiste en plusieurs exercices couvrant les domaines cités ci-dessus, où les étudiants sont appelés à résoudre des problèmes en utilisant des méthodes analytiques, géométriques, et probabilistes.
Ce programme vise à développer les compétences analytiques, géométriques et statistiques des élèves tout en les préparant aux exigences des études supérieures en sciences et technologies.

Tout savoir sur le jeûne du Ramadan
Le jeûne du Ramadan est un pilier fondamental de l'Islam. Il est pratiqué par les musulmans du monde entier pendant le neuvième mois du calendrier islamique, qui dure environ 29 ou 30 jours.
Par Abdoulaye OUEDRAOGO
Les opportunités d'entrepreneuriat en Afrique
Ce cours vous donne des idées de business et des guides pratiques pour aider toute personne désirant entreprendre en Afrique sans même trop dépensé.
Par Abdoulaye OUEDRAOGO